


Next: Detection Problem
Up: Decoding From Spike Trains
Previous: Decoding From Spike Trains
Suppose that we have a population
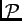 of an arbitrary number of
neurons
of an arbitrary number of
neurons 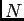 . Suppose that the population responds to a time dependent scalar
variable
. Suppose that the population responds to a time dependent scalar
variable 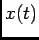 by producing a number of spike trains as shown by Fig.
1, i.e.
by producing a number of spike trains as shown by Fig.
1, i.e.
Figure 1:
Population of neurons
 |
where
and 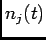 is the total number of spikes produced by the
is the total number of spikes produced by the
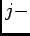 th neuron
in the interval
th neuron
in the interval ![$ [0, t]$](img9.png) . We allow the possibility of
. We allow the possibility of  , in which case
, in which case
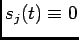 .
.
Let us suppose that the population acts with a certain degree of randomness,
i.e.
the repetition of the same 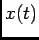 does not produce identical response.
Assuming that the collection of spike trains carries ``enough'' information
about
does not produce identical response.
Assuming that the collection of spike trains carries ``enough'' information
about 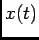 (i.e.
(i.e. 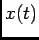 is encoded in the spike trains), we can ask the
following question: How would one decode an arbitrary function of
is encoded in the spike trains), we can ask the
following question: How would one decode an arbitrary function of 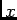 (and
in particular
(and
in particular 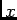 itself) from the spike train observations?
itself) from the spike train observations?



Next: Detection Problem
Up: Decoding From Spike Trains
Previous: Decoding From Spike Trains
Zoran Nenadic
2002-07-18

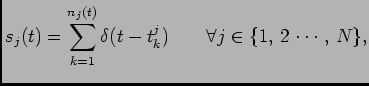
![]() does not produce identical response.
Assuming that the collection of spike trains carries ``enough'' information
about
does not produce identical response.
Assuming that the collection of spike trains carries ``enough'' information
about ![]() (i.e.
(i.e. ![]() is encoded in the spike trains), we can ask the
following question: How would one decode an arbitrary function of
is encoded in the spike trains), we can ask the
following question: How would one decode an arbitrary function of ![]() (and
in particular
(and
in particular ![]() itself) from the spike train observations?
itself) from the spike train observations?