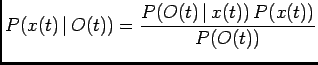Next: Decoding Algorithm
Up: Decoding From Spike Trains
Previous: Introduction
Let 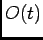 be the observed response of the population
be the observed response of the population
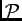 to a time
varying scalar function
to a time
varying scalar function 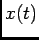 . In general
. In general 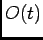 can be any set of features
of the response
can be any set of features
of the response 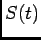 .
Using Bayes' rule one can easily write
.
Using Bayes' rule one can easily write
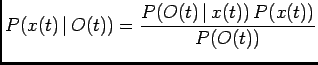 |
(1) |
If 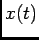 takes values from a discrete set of functions
takes values from a discrete set of functions
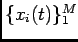 ,
we can formulate the following detection problem
,
we can formulate the following detection problem
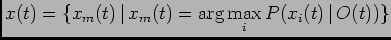 |
(2) |
The idea given by (2) is not a new one and has been extensively
used for various applications. For example, if
where 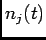 is the number of spikes fired by
is the number of spikes fired by
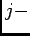 th neuron in time
interval
th neuron in time
interval ![$ [0, t]$](img9.png) , one has so-called rate decoding. Since neurons fire
with a considerable degree of variability, one might argue that the precise
spike timings are not important in the encoding process, and that the idea of
rate decoding is justified. However, this encoding/decoding scheme is not very
efficient, especially if the firing rates of neurons within the population are
not sufficiently high. Assuming the signals are encoded in a sequence of
spike times
, one has so-called rate decoding. Since neurons fire
with a considerable degree of variability, one might argue that the precise
spike timings are not important in the encoding process, and that the idea of
rate decoding is justified. However, this encoding/decoding scheme is not very
efficient, especially if the firing rates of neurons within the population are
not sufficiently high. Assuming the signals are encoded in a sequence of
spike times
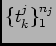 increases the information
capacity of the population
increases the information
capacity of the population
 tremendously. Here, we propose the
decoding method that is based on full statistical description of the population
response, namely we assume that
tremendously. Here, we propose the
decoding method that is based on full statistical description of the population
response, namely we assume that 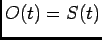 .
.



Next: Decoding Algorithm
Up: Decoding From Spike Trains
Previous: Introduction
Zoran Nenadic
2002-07-18